问题详情

两个矩阵Am*n和Bn*p相乘，用基本的方法进行，则需要的乘法次数为m*n*p 多个矩阵相乘满足结合律，不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M{i+i)，…，Mj多个矩阵连乘的最优顺序，即所需要的乘法次数最少。最少乘法次数用m[i，j]表示，其递归式定义为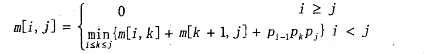：其中i、j和k为矩阵下标，矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序，其时间复杂度为(64 )。若四个矩阵M1. M2、M3.，M4相乘的维度序列为2、6、3、10.3，采用上述算法求解，则乘法次数为(65 )。

A.O(N2)

B.O(N2Lgn)

C.O(N3)

D.O(n3lgn)

请帮忙给出正确答案和分析，谢谢！